- 110
		- 111
			- 1111平面点集的基本概念
			- 1112二元函数的极限
				- 11.3二元函数的连续
			- 1113二元函数的连续
			- 1114二元函数的偏导数
				- 11.2二元函数的偏导数
			- 1115多元函数可微
			- 1116多元函数偏导数连续性
		- 112
			- 1121链式求导
				- 11.5二阶连续偏导数
			- 1122隐函数存在定理
				- 11.6隐函数求偏导
				- 11.9全微分
				- 11.10给出偏微分方程反求表达式
				- 11.9*
		- 113
			- 1131多元函数极值和最值的概念
			- 1132无条件极值
				- 11.11无条件极值
				- 11.12 公式法失效
			- 1133条件极值和拉格朗日乘法
				- 11.14 条件极值
				- 11.15 闭区域最值

110

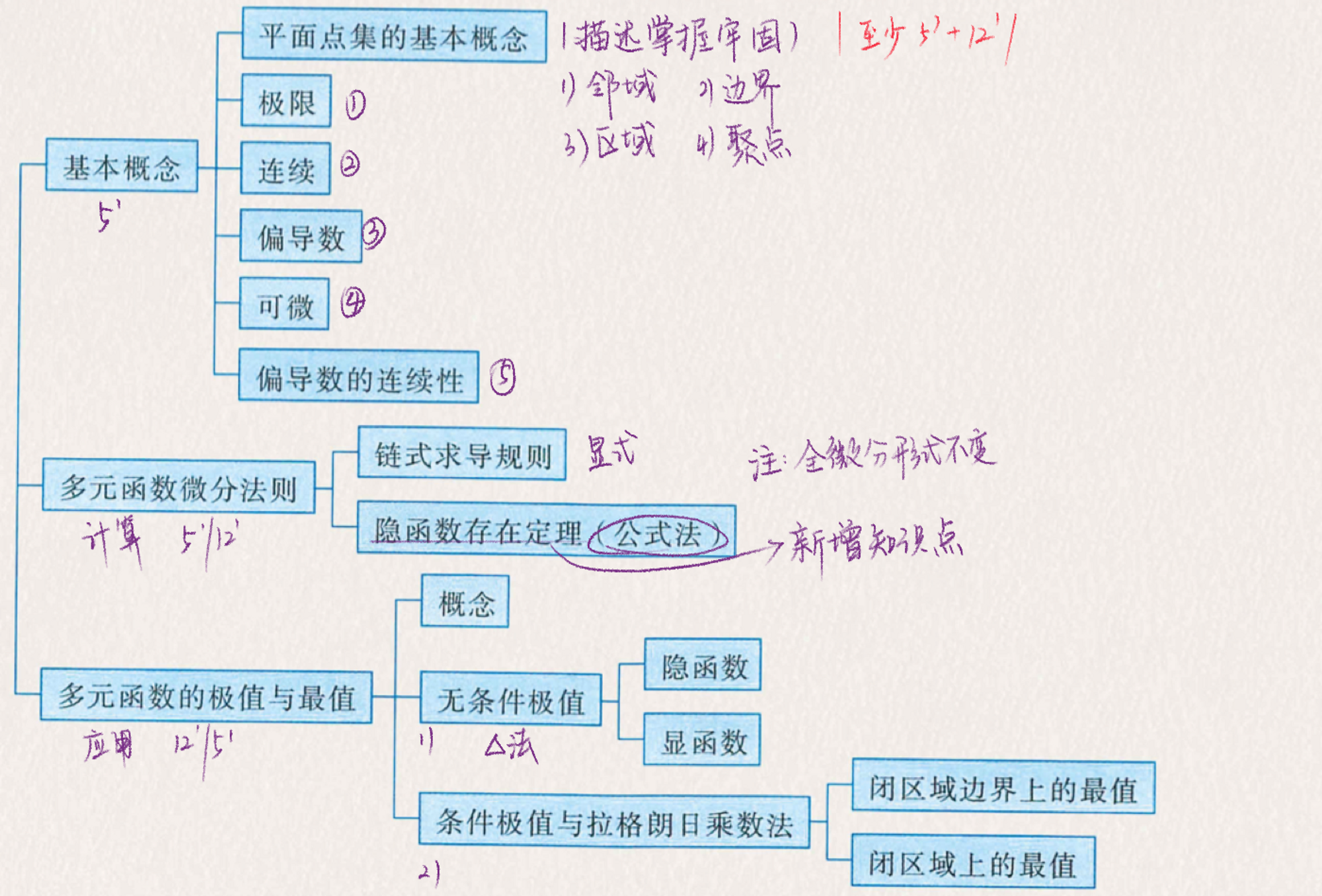
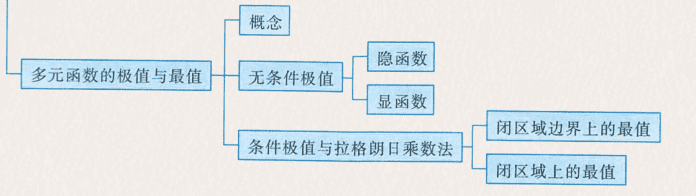
• 知识框架如图所示，包括需要了解基本概念，这里可能会有 5 分，多元函数的微分法则，多元函数的极值与最值需要重点关注。

111

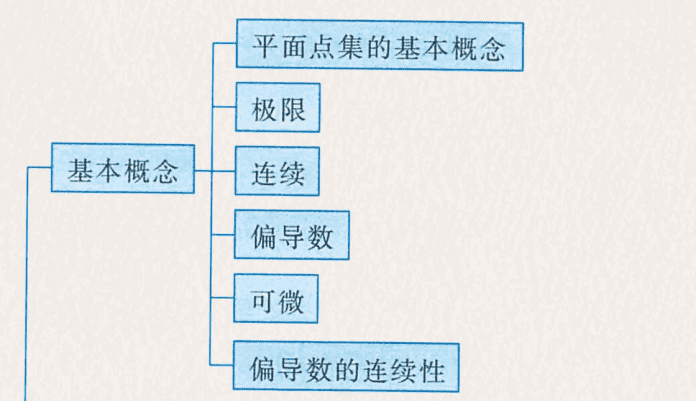
1111 平面点集的基本概念

• 了解基本概念

• 对点集进行分类，进行概念理解

• 注意去心邻域概念；内点、外点、边界点的概念；

1112 二元函数的极限

• 关于函数极限有下面两种定义，注意区别

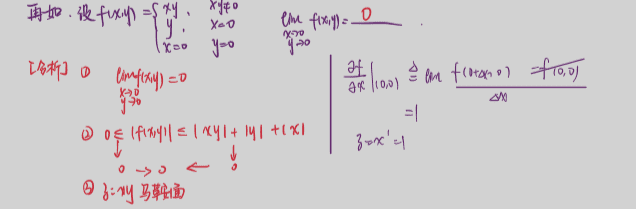
11.3 二元函数的连续

1113 二元函数的连续

• 二元函数的连续和一元函数对比记忆

1114 二元函数的偏导数

• 偏导数的意思就是走特殊路径，有失偏颇

11.2 二元函数的偏导数

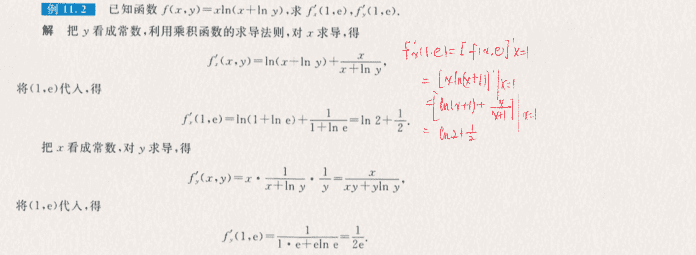
1115 多元函数可微

• 多元函数可微分的定义

1116 多元函数偏导数连续性

• 定义法+公式法

112

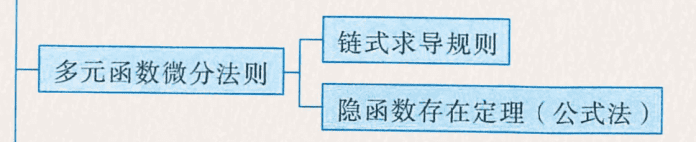
1121 链式求导

• 理解附注当中的含义

11.5 二阶连续偏导数

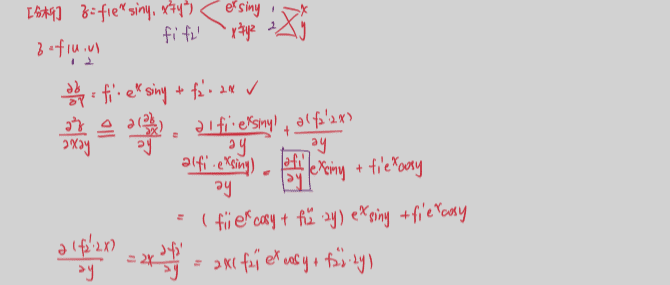
1122 隐函数存在定理

• 隐函数存在定理

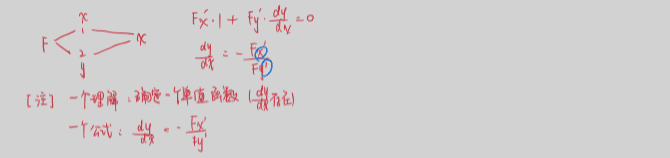
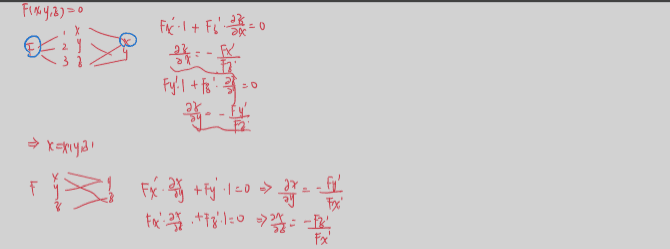
11.6 隐函数求偏导

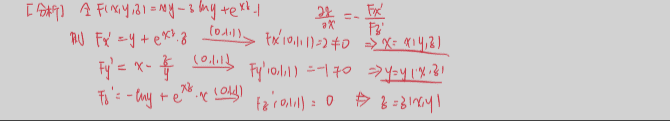
11.9 全微分

11.10 给出偏微分方程反求表达式

11.9

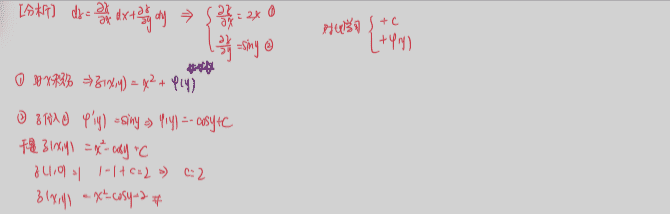
113

1131 多元函数极值和最值的概念

• 最值的概念是比较出来的

1132 无条件极值

• 用公式法求二元函数的极值 11.11 无条件极值

11.12 公式法失效

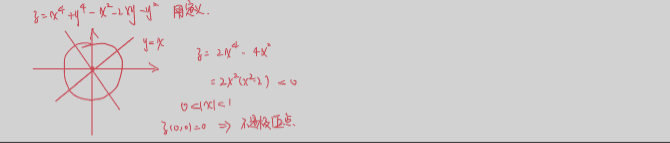
1133 条件极值和拉格朗日乘法

• 关注解题步骤

11.14 条件极值

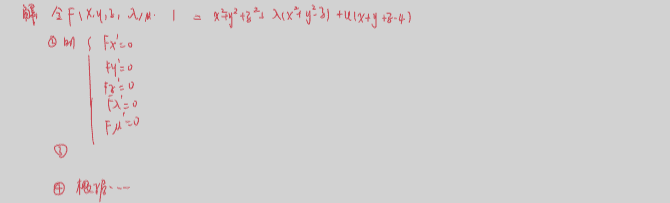
11.15 闭区域最值